In probability theory and statistics, many real-world problems revolve around events that can result in just two outcomes: success or failure. These events can be as simple as flipping a coin or as complex as classifying an email as spam or not. At the core of such binary outcomes lies a fundamental probability model known as the Bernoulli distribution.

This distribution provides a way to model and understand events that have only 2 possible outcomes, typically labeled as 1 (success) and 0 (failure). It is one of the most basic and foundational distributions in the world of statistics and plays an essential role in both academic learning and practical applications.

Defining the Bernoulli Distribution

The Bernoulli distribution is a discrete probability distribution for a random variable, which takes the value 1 with probability p (representing success) and the value 0 with probability 1 - p (representing failure).

This model applies to a single trial or experiment where there are only two outcomes. The probability of success, p, must lie between 0 and 1. Likewise, the probability of failure becomes 1 - p, ensuring that the total probability remains 1.

Bernoulli Random Variable

A random variable that follows a Bernoulli distribution is referred to as a Bernoulli random variable. For example, when tossing a coin:

• Getting heads can be marked as 1 (success)
• Getting tails can be marked as 0 (failure)

This single-trial experiment perfectly fits the definition of a Bernoulli distribution.

Mathematical Representation

The probability mass function (PMF) of a Bernoulli distribution is:

P(X = x) = pˣ × (1 - p)¹⁻ˣ

Where:

• X is a Bernoulli random variable (either 0 or 1)
• x is the specific outcome (0 or 1)
• p is the probability of success (0 ≤ p ≤ 1)

Using this formula:

• If x = 1 (success), then P(X = 1) = p
• If x = 0 (failure), then P(X = 0) = 1 - p

It makes the Bernoulli distribution both intuitive and easy to calculate for binary scenarios.

Properties of the Bernoulli Distribution

Several statistical properties make the Bernoulli distribution useful:

• Mean (Expected Value): E[X] = p. It indicates the average number of successes expected in many repeated trials.
• Variance: Var(X) = p(1 - p). It shows how much the results will vary around the mean.
• Skewness: The distribution is symmetric when p = 0.5, skewed right if p < 0.5, and skewed left if p > 0.5.
• Support: The distribution only takes on two values: 0 and 1.
• Kurtosis: Kurtosis can be derived from the variance and skewness but isn't commonly used with such a simple distribution.

These properties help in making decisions and drawing conclusions from binary data.

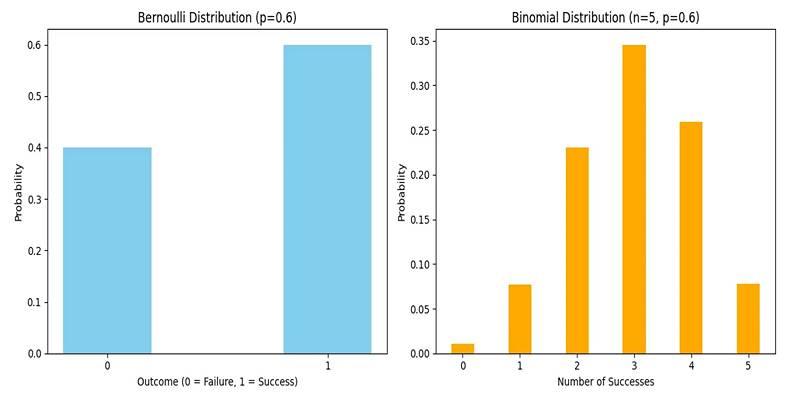
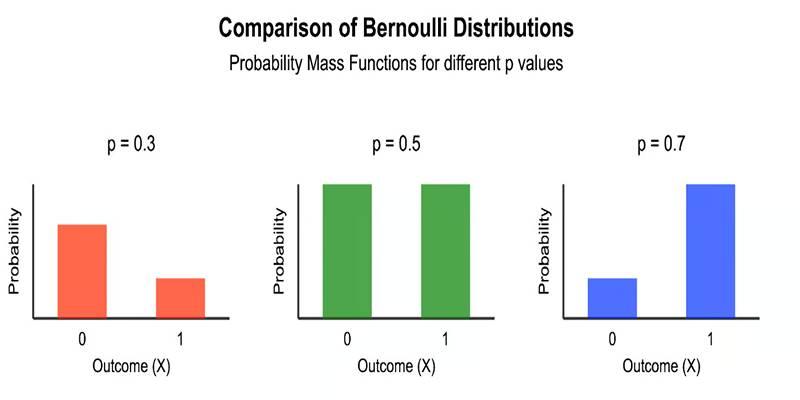
Visualizing the Bernoulli Distribution

The Bernoulli distribution can be visualized using a simple bar graph with two bars:

• One bar at x = 0 with height 1 - p
• One bar at x = 1 with height p

Example:

If p = 0.8, the graph will show a taller bar at x = 1 and a shorter bar at x = 0.
If p = 0.3, the situation reverses, and x = 0 becomes the taller bar.

The shape of the graph instantly tells how likely success is compared to failure.

Real-Life Applications of Bernoulli Distribution

Though theoretical in form, the Bernoulli distribution is extremely applicable in real-life settings where binary decisions are made regularly. Below are several scenarios where this model is used.

Quality Control in Manufacturing

A company producing lightbulbs may test each one to determine whether it works (success = 1) or doesn’t (failure = 0). Each test on a single bulb follows a Bernoulli distribution, and the results can be used to determine the quality of production.

Marketing and Customer Behavior

In marketing, businesses often track whether a user clicks on an advertisement (click = 1) or not (no click = 0). This behavior is modeled using a Bernoulli distribution, especially when analyzing single-ad interactions.

Medical Trials

In clinical research, each patient’s response to a new drug might be recorded as either a success (positive response = 1) or failure (no response = 0). Each patient’s outcome is a Bernoulli trial.

Binary Classification in Machine Learning

Many machine learning models deal with problems that have two classes—spam or not spam, fraud or not fraud, and so on. Each prediction in these models can be framed as a Bernoulli-distributed output.

Mathematical Expectations and Variance

Understanding the mean and variance of a Bernoulli distribution helps in analyzing its behavior:

• Mean (μ): The mean of the distribution is simply p, the probability of success. It tells how often success is expected over many repeated trials.
• Variance (σ²): Calculated as p(1 - p), the variance shows the degree of variability in the distribution. When p is near 0.5, the variance is highest.

When to Use the Bernoulli Distribution

The Bernoulli model is appropriate when:

• There is a single experiment or trial
• Only two outcomes are possible
• The probability of success is known or can be estimated
• Repeated independent trials are not required (for that, use the Binomial distribution)

It is especially useful in early-stage analysis, where binary decisions are made.

Why Bernoulli Distribution Matters?

Even though the Bernoulli distribution is basic, it serves as a building block for several advanced statistical models and algorithms. Its simplicity makes it ideal for beginners, and its applicability extends to many professional domains.

Key Areas of Use:

• Foundational theory for binomial and geometric distributions
• Machine learning models like logistic regression
• Survey analysis, where answers are often "Yes" or "No"
• Financial decisions, like success/failure of trades

Conclusion

The Bernoulli distribution is not just an academic concept—it’s a practical tool used across industries and disciplines. Whether in business, science, or technology, any scenario involving a simple yes-or-no result can be effectively modeled using this distribution. Its clear definition, easy-to-use formula, and wide range of applications make it one of the most essential concepts in probability theory. By mastering the Bernoulli distribution, learners gain a firm foundation to explore more complex statistical models and understand real-world binary decisions with confidence.